__________
小学习数学小学六年级下册要点总结
第一单元 负数
__________
负数的起源
为了表示相反意义的两个量（如盈利亏损、收入支出……），仅有学过的0，1 ，3.4，
……是远远不够的，所以出现了负数，以盈利为正、亏损为负；以收入为正、支出为负。
2.负数
小于0的数叫做负数，像—1、—5、—3、—0.7、—
等如此的数是负数，负数有无数个。
3.正数
大于0的数叫做正数，像+5、8、63、+4.1、等如此的数是正数，正数有无数个。
4.正、负数的读写办法
（1）写正数时，数字前面可以加正号“+”，也可以省略不写；读正数时，带“+”的必须要读出“正”字，省略“+”的，这个“正”字就不读出来。
（2）写负数时，数字前面加负号“—”，不能省略；读负数时，必须要读出“负”字。
【要素提示】
☀0不是正数，更不是负数，它是正数与负数的分界点。
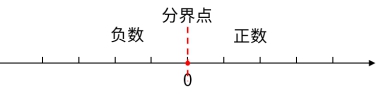5.用数轴表示数
负数 0 正数
左侧 < 右边
【要素提示】
☀直线上的数越往右越大，越往左越小。
6.比较两数的大小
①借助数轴：负数＜0＜正数 或 左侧＜右侧
②借助正负数的意思：
正数之间比较大小，数字大的就大，数字小的就小；
负数之间比较大小，数字大的反而小，数字小的反而大。
第二单元 百分数
__________
打折
（1）打折的意义
为了吸引客户，促进客户购物消费，商店有时降价供应产品，叫做优惠扣销售，俗称“优惠”。几折表示十分之几，也就是百分之几十；几几折表示十分之什么时间几，也就是
百分之几十几。
（2）与打折有关的实质问题的解题办法
❶已知原价和打折，求现价：现价=原价×打折
❷已知原价和打折，求实惠的钱数：实惠的钱数=原价－原价×打折或实惠的钱数=原价×。
❸已知现价和打折，求原价：依据“原价×打折=现价”列方程解答；或者依据“原价=现价÷打折”直接列算式解答。
【要素提示】
☀打几折就是按原价的百分之几十供应，而不是价格降低了原价的百分之几十。
2.成数
（1）成数的意义
成数表示一个数是另一个数的十分之几，通称“几成”。
（2）成数问题的解题办法
解决成数问题时，把成数转化为百分数后，解题思路和办法与百分数问题一模一样。
【要素提示】
☀解决成数问题的重点是先将成数转化为百分数或分数。
3.税率
（1）税收的有关定义
❶纳税：纳税是依据国家税法的有关规定，根据肯定的比率把集体或个人收入的一部分缴纳给国家。
❷税款：单位或个人收入中的一部分要上缴给国家，上缴的钱叫做税款，缴纳的税款叫做应纳税额。
❸税率：应纳税额与各种收入（销售额、营业额……）的比率叫做税率。
（2）纳税的意义
税收是国家财政收入的主要来源之一。国家用收来的税款进步经济、科技、教育、文化和国防安全等事业。
（3）应纳税额的求法：应纳税额=收入额×税率
（4）税率的求法：税率=应纳税额÷收入额×100%
（5）收入额的求法：收入额=应纳税额÷税率
【要素提示】
☀税收的类型不同，税率也各不相同，每种税的税率都是由国家规定的。
4.利率
（1）储蓄的意义
大家常常把暂时不需要的钱存入银行或信用社储蓄起来，如此不仅能够支援国家建设，也使得个人用钱愈加安全和有计划，还可以增加一些收入。
（2）存款的方法
活期
整存整取
零存整取
（3）储蓄的有关定义
❶本金：存入银行的钱叫做本金。
❷利息：取款时银行多支付的钱叫做利息。
❸利率：单位时间（如1年、1月、1日等）内的利息与本金的比率叫做利率。
❹利息的计算办法：利息=本金×利率×存期
【要素提示】
☀假如要缴纳利息税，则：税后利息=本金×利率×存期×。
第三单元 圆柱与圆锥
__________
1.圆柱的认识
（1）圆柱的特点
❶圆柱是由两个底面和一个侧面围成的，它的底面是大小相同的两个圆，侧面是一个曲面。
❷圆柱的侧面沿高展开后是一个长方形，这个长方形的一边长等于圆柱的底面周长，另一边长等于圆柱的高。
（2）圆柱的高
❶圆柱的两个底面之间的距离叫做高。
❷圆柱有无数条高。
【要素提示】
☀当圆柱的底面周长和高相等时，它的侧面沿高展开后是一个正方形。
☀圆柱的侧面展开图可能是长方形或正方形，也会是平行四边形，不可能是梯形。
2.圆柱的表面积
（1）圆柱的侧面积公式：圆柱的侧面积=底面周长×高，用字母表示为S=Ch=2πrh。
（2）圆柱的表面积公式：圆柱的表面积=侧面积+底面积×2，用字母表示为S=2πrh+2πr²。
【要素提示】
☀求圆柱形通风管、笔筒或水桶的表面积时，应该注意底面的个数。
3.圆柱的体积
圆柱体积的计算公式：圆柱的体积=底面积×高，用字母表示为V=Sh=πr²h。
4.圆锥的认识
（1）圆锥的特点
圆锥是由一个底面和一个侧面围成的，它的底面是一个圆，侧面是一个曲面。
（2）圆锥的高
❶从圆锥的顶点到底面圆心的距离是圆锥的高。
❷圆锥只有一条高。
【要素提示】
☀圆锥的侧面展开图是一个扇形。
5.圆锥的体积
（1）圆锥的体积等于与它等底等高的圆柱体积的
。
（2）圆锥的体积计算公式：圆锥的体积=底面积×高×，用字母表示为V= Sh。
【要素提示】
☀把一个圆柱削成一个最大的圆锥，这个圆锥与圆柱等底等高。
第四单元 比率
__________
1.比率的意义：表示两个比相等的式子叫做比率。
2.比率基本性质：在比率里，两个外项的积等于两个内项的积。
3.解比率：求比率中未知项的过程，叫做解比率。
【要素提示】
☀依据比率的意义和比率的基本性质可以判断两个比能否组成比率。
☀比和比率有什么区别：
（1）比表示两个数相除，它有两项（即前项和后项）；比率表示两个比相等，它有四项（即两个内项和两个外项）。
（2）比有基本性质，它是化简比的依据；比率也有基本性质，它是解比率的依据。
4.正比率
（1）正比率的意义
两种有关联的量，一种量变化，另一种量也伴随变化，假如这两种量中相对应的两个数的比值肯定，这两种量就叫做成正比率的量，它们的关系叫做正比率关系。字母关系式为
=k（肯定）。
（2）正比率关系的图像
正比率图像是一条从原点出发的无限延伸的射线，线上所有点所对应的两个数的比值都相等。
（3）判断两种量是不是成正比率的办法
先找变量（找两种有关联的量），再看定量（看两种量中相对应的两个数的比的比值是不是肯定），最后作出判断。
5.反比率
（1）反比率的意义
两种有关联的量，一种量变化，另一种量也伴随变化，假如这两种量中相对应的两个数的乘积肯定，这两种量就叫做成反比率的量，它们的关系叫做反比率关系。字母关系式为xy=k（肯定）。
（2）判断两种量是不是成反比率的办法
重点看这两种有关联的量中相对应的两个数的乘积是不是肯定，假如肯定，就成反比率。
【要素提示】
☀成比率的两种量需要是有关联的量，而两种有关联的量却未必都成比率。
6.用比率解决问题
依据问题中的不变量找出两种有关联的量，并判断这两种有关联的量成什么比率关系，再依据正、反比率关系列出相应的比率并求解。
【要素提示】
☀用正、反比率解决问题的重点是确定成什么比率关系。
7.比率尺
（1）比率尺的意义
一幅图的图上距离和实质距离的比，叫做这幅图的比率尺。
（2）比率尺的分类
❶按表现形式分，可以分为数值比率尺和线段比率尺。
❷按将实质距离缩小还是放大分，可以分为缩小比率尺和放大比率尺。
【要素提示】
☀比率尺是一个比，表示两个相同种类量间的倍比关系，不可以带单位名字。
（3）已知图上距离和实质距离，求比率尺的办法
先把图上距离和实质距离统一单位，再用图上距离比实质距离，然后把它化简成前项是1或者后项是1的比，得出比率尺。
（4）已知比率尺和图上距离，求实质距离的办法
可以参考“图上距离：实质距离=比率尺”用解比率的办法求出实质距离，也可以借助“实质距离=图上距离÷比率尺”直接列式计算。
（5）已知比率尺和实质距离，求图上距离的办法
可以参考“图上距离：实质距离=比率尺”用解比率的办法求出图上距离，也可以借助“图上距离=实质距离×比率尺”直接列式计算。
8.图形的放大与缩小
（1）特征：形状相同，大小不同。
（2）将图形放大或缩小的办法
一看，看原图形各边占几格；
二算，按已知比计算出放大图或缩小图的各边占几格；
三画，按计算出的边长画出原图形的放大图或缩小图。
【要素提示】
☀把图形每条边按相同倍数放大后，形状不变，相对应的角的度数也不变。
第五单元 鸽巢问题
__________
1.“鸽巢原理”：
把m个物体任意分放进n个鸽巢中，那样肯定有一个鸽巢中至少放进了2个物体。
2.“鸽巢原理”：
把多于kn个的物体任意分放进n个鸽巢中，那样肯定有一个鸽巢中至少放进了个物体。
3.应用“鸽巢原理”解题的一般步骤：
①剖析题意，把实质问题转化成“鸽巢问题”，即弄清“鸽巢”和分放的物体；
②设计“鸽巢”的具体形式；
③运用原理得出在某个“鸽巢”中至少分放的物体个数，最后解决问题。
